5.1 Elementos características y componentes de los grafos

5.1 Elementos y Características de los Grafos

A partir de esta figura se definen los siguientes elementos:

Vértices (nodos) 

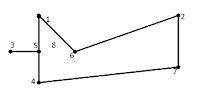
Se indican por medio de un pequeño círculo y se les asigna un número o letra. En el grafo anterior los vértices son V= {a, b, c, d}.

Lados (ramas o aristas)

Son las líneas que unen un vértice con otro y se les asigna una letra, un numero o una combinación de ambos. En el grafo anterior los lados son:

L= {1, 2, 3, 4, 5, 6}.

Lados paralelos

Son aquellas aristas que tienen relación con un mismo par de vértices. En el grafo anterior los lados paralelos son: P= {2,3}.

Lazo

Es aquella arista que sale de un vértice y regresa al mismo vértice. En el grafo anterior se tiene el lazo: A= {6}

Valencia de un vértice

Es el número de lados que salen o entran a un vértice. En el grafo anterior las valencias de los vértices son:

Valencia (a)=2

Valencia (b)=4

Valencia (c)=2

Valencia (d)=3

Aristas:

Son las líneas con las que se unen las aristas de un grafo y con la que se construyen también caminos. Si la arista carece de dirección se denota indistintamente {a, b} o {b, a}, siendo a y b los vértices que une. Si {a, b} es una arista, a los vértices a y b se les llama sus extremos.

• Aristas Adyacentes: Se dice que dos aristas son adyacentes si convergen en el mismo vértice.

• Aristas Paralelas: Se dice que dos aristas son paralelas si vértice inicial y el final son el mismo.

• Aristas Cíclicas: Arista que parte de un vértice para entrar en el mismo.

• Cruce: Son dos aristas que cruzan en un punto.

Vértices:

Son los puntos o nodos con los que está conformado un grafo. Llamaremos grado de un vértice al número de aristas de las que es extremo. Se dice que un vértice es `par' o `impar' según lo sea su grado.

• Vértices Adyacentes: si tenemos un par de vértices de un grafo (U, V) y si tenemos un arista que los une, entonces U y V son vértices adyacentes y se dice que U es el vértice inicial y V el vértice adyacente.

• Vértice Aislado: Es un vértice de grado cero.

• Vértice Terminal: Es un vértice de grado 1.

Matematicas Discretas. (s.f.). Obtenido de Matematicas Discretas: https://sites.google.com/site/matedicreta/6-1-elementos-y-caracteristicas-de-los-grafos

Matematicas Discretas. (s.f.). Obtenido de Matematicas Discretas: https://sites.google.com/site/matedicreta/6-1-1-componentes-de-un-grafo

5.3.3 En profundidad

5.3.3 En profundidad

Una Búsqueda en profundidad es un algoritmo que permite recorrer todos los nodos de un grafo o árbol (teoría de grafos) de manera ordenada, pero no uniforme. Su funcionamiento consiste en ir expandiendo todos y cada uno de los nodos que va localizando, de forma recurrente, en un camino concreto. Cuando ya no quedan más nodos que visitar en dicho camino, regresa (Backtracking), de modo que repite el mismo proceso con cada uno de los hermanos del nodo ya procesado..  

Pseudocodigo algoritmo búsqueda en profundidad

funcion buscar_en_hijos(Nodo:n)

variable encontrado=boolean

inicio

    si solucion(n->hijo)

    retornar n->hijo

    

    sino

    n1=n->hijo

    encontrado=falso    

        mientras no (encontrado)

        n1=n1->hermano

        sisolucion(n1)

        retornar n1

        

        sino

            n1=null

            romper ciclo

    

            buscar_en_hijos(n->hijo)

            n2->n->hijo

    

                mientras(n2->hermano!=null)

                n2=n2->hermano

                buscar_en_hijos(n2)

        fin si

    fin mientras

fin función

GOMEZ, D. R. (s.f.). Inteligencia Artificial. Obtenido de Inteligencia Artificial: https://sites.google.com/a/utp.edu.co/inteligencia-artificial/algoritmo-busqueda-en-profundidad

5.3.2 A lo ancho

5.3.2 A lo ancho

En ciencias de la computación, A * (pronunciado “Una estrella” (escuchar)) es un algoritmo informático que se utiliza amplia mente en la búsqueda de caminos y el recorrido del grafo, el proceso de trazar un camino transitable de manera eficiente entre los puntos, llamados nodos. Destaca por su rendimiento y precisión, que goza de amplio uso. (Sin embargo, en los sistemas de los viajes de enrutamiento prácticos, generalmente superado por algoritmos que pueden pre-procesar la gráfica para lograr un mejor rendimiento.) 

Ejemplo:

Un ejemplo de una estrella (A *) algoritmo en acción donde los nodos son las ciudades conectadas con carreteras y h (x) es la distancia en línea recta al punto de destino: 

Clave: verde: inicio, el azul: objetivo, de color anaranjado: visited 

Nota: En este ejemplo se utiliza una coma como separador decimal. 

Ilustración de la búsqueda A * para la búsqueda de ruta desde un nodo de inicio a un nodo objetivo en un robot de planificación de movimientos problema. 

Una búsqueda de * que utiliza una heurística que es de 5,0 (= ε) veces a la heurística consistente, y obtiene una ruta subóptima. 

SAUCEDO, F. E. (s.f.). Matematicas Discretas. Obtenido de Matematicas Discretas: https://sites.google.com/site/matedicreta/ 6-3-2-a-lo-ancho

5.3.1 El camino mas corto

5.3.1 El camino más corto

El problema de los caminos más cortos es el problema que consiste en encontrar un camino entre dos vértices (o nodos) de tal manera que la suma de los pesos de las aristas que lo constituyen es mínima.

En la teoría de grafos, el problema del camino más corto es el problema que consiste en encontrar un camino entre dos vértices (o nodos) de tal manera que la suma de los pesos de las aristas que lo constituyen es mínima. Un ejemplo de esto es encontrar el camino más rápido para ir de una ciudad a otra en un mapa. En este caso, los vértices representarían las ciudades y las aristas las carreteras que las unen, cuya ponderación viene dada por el tiempo que se emplea en atravesarlas. Lo constituyen es mínima.

Ejemplo:

Un ejemplo de una estrella (A *) algoritmo en acción donde los nodos son las ciudades conectadas con carreteras y h (x) es la distancia en línea recta al punto de destino: 

Clave: verde: inicio, el azul: objetivo, de color anaranjado: visited 

Nota: En este ejemplo se utiliza una coma como separador decimal

SAUCEDO, F. E. (s.f.). Matematicas Discretas. Obtenido de Matematicas Discretas: https://sites.google.com/site/matedicreta/6-3-1-el-camino-mas-corto

5.3 Algoritmo de recorrido y busqueda

 5.3 Algoritmo de recorrida y busqueda

Al visitar los nodos de un árbol existen algunas maneras útiles en las que se pueden ordenar sistemáticamente los nodos de un árbol.

Los ordenamientos más importantes son llamados: preorden, post-orden y en-orden y se definen recursivamente como sigue:

Si un árbol T es nulo, entonces, la lista vacía es el listado preorden, post-orden y en-orden del árbol T.

Si T consiste de un sólo nodo n, entonces, n es el listado preorden, post-orden y en-orden del árbol T.

Los algoritmos de recorrido de un árbol binario presentan tres tipos de actividades comunes:

• visitar el nodo raíz

• recorrer el subárbol izquierdo

• recorrer el subárbol derecho

Estas tres acciones llevadas a cabo en distinto orden proporcionan los distintos recorridos del árbol.

Recorrido en PRE-ORDEN:

• Visitar el raíz

• Recorrer el subárbol izquierdo en pre-orden

• Recorrer el subárbol derecho en pre-orden

Recorrido EN-ORDEN

• Recorrer el subárbol izquierdo en en-orden• Visitar el raíz• Recorrer el subárbol derecho en en-orden

Recorrido en POST-ORDEN

• Recorrer el subárbol izquierdo en post-orden

• Recorrer el subárbol derecho en post-orden

• Visitar el raíz

Recorridos

Si T es un árbol con raíz n y subárboles T1, T2, . . . , Tk, entonces, El listado pre-orden de los nodos de T es la raíz n, seguida por los nodos de T1 en pre-orden, después los nodos de T2 en preorden, y así, hasta los nodos de Tk en pre-orden.

El listado post-orden de los nodos de T es los nodos de T1 en postorden, seguidos de los nodos de T2 en post-orden, y así hasta los nodos de Tk en post-orden, todos ellos seguidos de n. El listado en-orden de los nodos de T es los nodos de T1 en-orden, seguidos por n, seguidos por los nodos de T2, . . . , Tk, cada grupo.

Recorreremos el Árbol Siguiente:

Recorrido Pre Orden (RID)

El recorrido en Pre Orden del árbol es el siguiente: 15, 6, 4, 10, 20, 17, 22

Recorrido En Orden(IRD)

El recorrido en En Orden del árbol es el siguiente: 4, 6, 10, 15, 17, 20, 22

Recorrido Post Orden(IDR)

El recorrido en Post Orden del árbol es el siguiente: 4, 10, 6, 17, 22, 20, 15

En este tema trataremos las diferentes formas de hacer recorridos de un árbol de una expresión algebraica, con el fin de poder cambiar de manera algorítmica una expresión en sufijo a forma de prefijo o posfijo.

Se llama recorrido de un árbol al proceso que permite acceder una sola vez a cada uno de los elementos del árbol para examinar el conjunto completo. Primeramente se ven los algoritmos para construir el árbol, para la expresión dada en sufijo, prefijo o posfijo y también se presentan algoritmos para reconocer si una expresión está correcta cuando esta dada en prefijo o posfijo.

Recorridos

Al visitar los elementos de un árbol existen algunas maneras útiles en las que se pueden ordenar sistemáticamente. Los ordenamientos más importantes son llamados: prefijo, sufijo y posfijo.

Los algoritmos de recorrido de un árbol presentan tres tipos de actividades

• visitar el nodo raíz
•  recorrer el subárbol izquierdo
• recorrer el subárbol derecho

Estas tres acciones llevadas a cabo en distinto orden proporcionan los distintos recorridos del árbol.

Recorrido en PREFIJO:

• Visitar la raíz
• Recorrer el subárbol izquierdo en prefijo
• Recorrer el subárbol derecho en prefijo

Recorrido SUFIJO:

• Recorrer el subárbol izquierdo en sufijo
• Visitar la raíz
• Recorrer el subárbol derecho en sufijo

Recorrido en POSFIJO:

• Recorrer el subárbol izquierdo en postfijo
• Recorrer el subárbol derecho en postfijo
• Visitar la raíz
• 
  

Flores, I. (22 de 11 de 2014). Relaciones y teoría de grafos. Obtenido de Relaciones y teoría de grafos.: http://equipo1mditq.blogspot.mx/2014/11/63-algoritmos-de-recorrido-y-busqueda.html 

5.2.2 Computacional

5.2.2 Computacional

Existen diferentes formas de almacenar grafos en una computadora. La estructura de datos, usada depende de las características del grafo y el algoritmo usado para manipularlo. Entre las estructuras más sencillas y usadas se encuentran las listas y las matrices y aunque frecuentemente se usa una combinación de ambos. 

SAUCEDO, F. E. (s.f.). Matematicas Discretas. Obtenido de Matematicas Discretas: https://sites.google.com/site/matedicreta/6-2-2-computacional

5.2.1 Matematica

5.2.2 Matematica

En matemáticas y ciencias de la computación, la teoría de grafos, también llamada teoría de las gráficas estudia las propiedades de los grafos (también llamados gráficas) Un grafo es un conjunto, no vacío, de objetos llamados vértices (o nodos) y una selección de partes de vértices llamados aristas. 

SAUCEDO, F. E. (s.f.). Matematicas Discretas. Obtenido de Matematicas Discretas: https://sites.google.com/site/matedicreta/6-2-1-matematica

5.1.1 Tipos de grafos

5.1.1 Tipos de grafos 

GRAFOS SIMPLES
Son aquellos grafos que no tienen lazos ni lados paralelos.

GRAFO COMPLETO DE N VÉRTICES (kn)
Es el grafo en donde cada vértice está relacionado con todos los demás sin lazos ni lados paralelos. Se indica como kn en donde n es el número de vértices del grafo.

La valencia en cada uno de los vértices de los grafos completos es (n – 1), y el número de lados está dado por la expresión
Núm. De lados = n(n – 1)
2
en donde n es el número de vértices del grafo.

COMPLEMENTO DE UN GRAFO (G‘)
Es el grafo que le falta al grafo G, de forma que entre ambos formas de grafo completo de n vértices. Este grafo no tiene lazos ni ramas paralelas.

GRAFO BIPARTIDO
es el grafo que está compuesta por dos conjuntos de vértices, A ={a1,a2, a3…, an} y B = {b1,b2,…, bm} en donde los elementos del conjunto B, pero entre los vértices de un mismo conjunto no existe arista que los una.

Una forma muy sencilla de saber si un grafo es bipartido es aplicar el hecho de que nunca tiene un ciclo de longitud impar, además de que debe cumplir con la característica mencionada anteriormente.

GRAFO BIPARTIDO COMPLETO (Kn, m) 
Es el grafo que está compuesto por dos conjuntos de vértices, uno de ellos A = {a1, a2, a3…, an} Y otro B= {b1,b2,…, bm), y en el cada vértice de A esta unido con todo los vértices de B, pero entre los vértices de un mismo conjunto no existe arista que los una. El grafo bipartido completo se indica Como kn, m.

Grafo plano

Un grafo G es plano si admite una representación en el plano de tal forma que las aristas no se cortan, salvo en sus extremos. A dicha representación se le denomina grafo plano. En teoría de grafos, un grafo plano (o planar según referencias) es un grafo que puede ser dibujado en el plano sin que ninguna arista se cruce (una definición más formal puede ser que este grafo pueda ser "incrustado" en un plano).

Grafos conexos

Un grafo es conexo (más formalmente fuertemente conexo) si todos sus vértices están conectados por un camino; es decir, si para cualquier par de vértices (a, b), existe al menos un camino posible desde a hacia b. Es posible determinar si un grafo es fuertemente conexo coleccionando la información de los grados de sus vértices al tiempo que se acumulan las diferentes rutas que salen de un vértice o llegan a él. En términos matemáticos la propiedad de un grafo de ser fuertemente conexo permite establecer en base a él una relación de equivalencia para sus vértices, la cual lleva a una partición de éstos en "componentes fuertemente conexos", es decir, porciones del grafo, que son fuertemente conexas cuando se consideran como grafos aislados. Esta propiedad es importante para muchas demostraciones en teoría de grafos.

Matematicas Discretas. (s.f.). Obtenido de Matematicas Discretas: https://sites.google.com/site/matedicreta/6-1-2-tipos-de-grafos

5.2 Representación de los grafos

5.2 Representación de los grafos

Matriz de adyacencia

1. Se crea una matriz cero, cuyas columnas y filas representan los nodos del grafo.
2. Por cada arista que une a dos nodos, se suma 1 al valor que hay actualmente en la ubicación correspondiente de la matriz.

Si tal arista es un bucle y el grafo es no dirigido, entonces se suma 2 en vez de 1.

Finalmente, se obtiene una matriz que representa el número de aristas (relaciones) entre cada par de nodos (elementos).

Existe una matriz de adyacencia única para cada grafo (sin considerar las permutaciones de filas o columnas), y viceversa.

Matriz de incidencia

1. Las columnas de la matriz representan las aristas del grafo.
2. Las filas representan a los distintos nodos.
3. Por cada nodo unido por una arista, ponemos un uno (1) en el lugar correspondiente, y llenamos el resto de las ubicaciones con ceros (0).

ejemplo:

SAUCEDO, F. E. (s.f.). Matematicas Discretas. Obtenido de Matematicas Discretas : https://sites.google.com/site/matedicreta/6-2-representacion-de-los-grafos