5.2.1 Matematica

5.2.2 Matematica

En matemáticas y ciencias de la computación, la teoría de grafos, también llamada teoría de las gráficas estudia las propiedades de los grafos (también llamados gráficas) Un grafo es un conjunto, no vacío, de objetos llamados vértices (o nodos) y una selección de partes de vértices llamados aristas. 

SAUCEDO, F. E. (s.f.). Matematicas Discretas. Obtenido de Matematicas Discretas: https://sites.google.com/site/matedicreta/6-2-1-matematica

5.1.1 Tipos de grafos

5.1.1 Tipos de grafos 

GRAFOS SIMPLES
Son aquellos grafos que no tienen lazos ni lados paralelos.

GRAFO COMPLETO DE N VÉRTICES (kn)
Es el grafo en donde cada vértice está relacionado con todos los demás sin lazos ni lados paralelos. Se indica como kn en donde n es el número de vértices del grafo.

La valencia en cada uno de los vértices de los grafos completos es (n – 1), y el número de lados está dado por la expresión
Núm. De lados = n(n – 1)
2
en donde n es el número de vértices del grafo.

COMPLEMENTO DE UN GRAFO (G‘)
Es el grafo que le falta al grafo G, de forma que entre ambos formas de grafo completo de n vértices. Este grafo no tiene lazos ni ramas paralelas.

GRAFO BIPARTIDO
es el grafo que está compuesta por dos conjuntos de vértices, A ={a1,a2, a3…, an} y B = {b1,b2,…, bm} en donde los elementos del conjunto B, pero entre los vértices de un mismo conjunto no existe arista que los una.

Una forma muy sencilla de saber si un grafo es bipartido es aplicar el hecho de que nunca tiene un ciclo de longitud impar, además de que debe cumplir con la característica mencionada anteriormente.

GRAFO BIPARTIDO COMPLETO (Kn, m) 
Es el grafo que está compuesto por dos conjuntos de vértices, uno de ellos A = {a1, a2, a3…, an} Y otro B= {b1,b2,…, bm), y en el cada vértice de A esta unido con todo los vértices de B, pero entre los vértices de un mismo conjunto no existe arista que los una. El grafo bipartido completo se indica Como kn, m.

Grafo plano

Un grafo G es plano si admite una representación en el plano de tal forma que las aristas no se cortan, salvo en sus extremos. A dicha representación se le denomina grafo plano. En teoría de grafos, un grafo plano (o planar según referencias) es un grafo que puede ser dibujado en el plano sin que ninguna arista se cruce (una definición más formal puede ser que este grafo pueda ser "incrustado" en un plano).

Grafos conexos

Un grafo es conexo (más formalmente fuertemente conexo) si todos sus vértices están conectados por un camino; es decir, si para cualquier par de vértices (a, b), existe al menos un camino posible desde a hacia b. Es posible determinar si un grafo es fuertemente conexo coleccionando la información de los grados de sus vértices al tiempo que se acumulan las diferentes rutas que salen de un vértice o llegan a él. En términos matemáticos la propiedad de un grafo de ser fuertemente conexo permite establecer en base a él una relación de equivalencia para sus vértices, la cual lleva a una partición de éstos en "componentes fuertemente conexos", es decir, porciones del grafo, que son fuertemente conexas cuando se consideran como grafos aislados. Esta propiedad es importante para muchas demostraciones en teoría de grafos.

Matematicas Discretas. (s.f.). Obtenido de Matematicas Discretas: https://sites.google.com/site/matedicreta/6-1-2-tipos-de-grafos

5.2 Representación de los grafos

5.2 Representación de los grafos

Matriz de adyacencia

1. Se crea una matriz cero, cuyas columnas y filas representan los nodos del grafo.
2. Por cada arista que une a dos nodos, se suma 1 al valor que hay actualmente en la ubicación correspondiente de la matriz.

Si tal arista es un bucle y el grafo es no dirigido, entonces se suma 2 en vez de 1.

Finalmente, se obtiene una matriz que representa el número de aristas (relaciones) entre cada par de nodos (elementos).

Existe una matriz de adyacencia única para cada grafo (sin considerar las permutaciones de filas o columnas), y viceversa.

Matriz de incidencia

1. Las columnas de la matriz representan las aristas del grafo.
2. Las filas representan a los distintos nodos.
3. Por cada nodo unido por una arista, ponemos un uno (1) en el lugar correspondiente, y llenamos el resto de las ubicaciones con ceros (0).

ejemplo:

SAUCEDO, F. E. (s.f.). Matematicas Discretas. Obtenido de Matematicas Discretas : https://sites.google.com/site/matedicreta/6-2-representacion-de-los-grafos

Introducción

En este blog aprenderemos sobre las los conjuntos ya que veremos varios conjuntos que no casi siempre serán iguales que otros lo cual incluye el conjunto vacío (represantado como cero cantidades) y el univreso ( el universo representa todos los numeros), después veremos  las relaciones que tienen dichos numeros o tipos de texto por el cual debemos de poner atencion como van a ir las realciones de cada unos de los ejercicios mostrados , aprederemos como utilizar los Diagramas de Venn como poder establezer su pocisión de los numeros.
Ahora bien las relaciones  los conjuntos se trabajan unidos, es decir , conjuntos contiene los elementos necesarios para poder establecer una relacion. Los conjuntos se pueden reprentar con {}
(dos llaves de abertura y cierre) que adentro contendra los elementos que contendra.

Asi que porfavor prestar mucha atención con los ejercicios que tenemos para mostrarles en este blog.

Ejercicios de conjuntos

Te presentamos los siguientes ejercicios de conjuntos porfavror ponen atención y con mucho en foque lo siguiente:


En los ejercicios del 1 – al  16 estableza el universo como un conjunto U {1,2,3,…..10}, sea A={1,4,7,10},

B={1,2,3,4,5} y C={4,6,8}. Liste los elementos de cada conjunto.

1.- A U B

A={1,4,7,10}

B={1,2,3,4,5}

A U B ={1,2,3,4,5,7,10}

2.- B ∩ C

B={1,2,3,4,5}

C={4,6,8}

B ∩ C = {2,4}

3.- A-B

A={1,4,7,10}

B={1,2,3,4,5}

A-B = {7,10}

4.-B-A

B={1,2,3,4,5}

A={1,4,7,10}

B-A = {2,3,5}

5.-A’

A={1,4,7,10}

A’ = {2, 3, 5, 6, 8, 9}

6.-U-C = {1, 2, 5, 7, 9, 10}

7.- Ū = {Ø}

8.- A – Ø = {1, 4, 7, 10, Ø}

9.- B ∩ Ø = {Ø}

10.-A∪U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}

11.-B ∩U = {1,2,3,4,5,6,7,8,9,10}

12.-A∩(B∪C)

A={1,4,7,10}

B={1,2,3,4,5}

C = {4,6,8}

= {1,2,3,4,5,6,8}

{1,4}

13.-B̅ ∩(C-A)

{2, 6, 8} {6, 7, 8, 9, 10}

            {6,8}

14.- (A ∩B)-C

{1}

15.-A̅ŪB̅ ∪ C

{6, 8, 9}∪ C
{2, 4, 6, 8}

16.- (A∪B)-(C-B)

A∪B = {1, 2, 3, 4, 5, 7, 10}  = {1,3, 4, 5, 7, 10}

Ejercicios en forma de texto u operaciones

Ejercicio 3.1.7

De 17 programas revisados en programación “C++”, 23 marcaron error en la complicación, 12 tuvieron fallas en lógica y 5 en lógica y compilación ¿Cuántos programas tuvieron al menos un tipo de error?

Ejercicio 3.1.8

En la biblioteca existen 103 libros de ciencias de la computación que trataban en cierta medida en los siguientes temas:

·        * Compiladores.

·        * Estructura de datos.

·        * Redes.

Del total, 50 libros tienen información sobre compiladores, 54 sobre estructura de datos,51 sobre redes, 30 sobre compiladores y estructura de datos, 32 sobre compiladores y redes, 34 sobre estructura de datos y redes y 19 de los 3 temas.

¿Cuántos libros tienen material exactamente sobre uno de los tres temas? 18

¿Cuántos no tienen de material de Redes? 26

¿Cuántos no tienen material sobre ninguno de los temas? 26

¿Cuántos libros contienen material de compiladores y redes pero de estructura de datos no? 23 

RELACIONES

En los ejercicios 1 al 4, escriba la relación como un conjunto de pares ordenados.

1.-

8840	Martillo
9921	Tenazas
452	Pintura
2207	Alfombra

A= {(8840 ,Martillo),(9921, Tenazas),(452,  Pintura),(2207, Alfombra)

2.-

a	3
b	1
b	4
c	1

A = {(a, 3), (b, 1), (b, 4), (c, 1)}

3.-

Susana	Matemáticas
Ruth	Física
Samuel	Economía

A = {(Susana, Matemáticas), (Ruth, Física), (Samuel, Economía)}

4.-

a	a
b	b

A = {(a, a), (b, b)}

En los ejercicio 5 al 8, escriba la relación como tabla.

5.-  R = {(a, 6),(b,2),(a,1),(c,1)}

a	6 , 1
b	2
c	1

6.-  R = {{Rogelio, Música}, (Patricia, Historia), (Benjamín, Matemáticas), (Patricia, Ciencias Políticas)}

Rogelio	Música
Patricia	Historia y ciencias políticas
Benjamín	matemáticas

7.-  La relación R en {1, 2, 3, 4} definida por if  x²  ≥ y

R = {(1,1),(2,1),(2,2).(3,1),(3,2)(3,3)(,4,1),(4,2),(,4,3,),(4,4)}

8.-  La relación R del conjunto X de planetas al conjunto Y de enteros definida por (x, y) ∈R si x está en la posición y respecto al sol (el más cercano al sol está en la posición 1, el segundo más cercano al sol está en la posición 2, y así sucesivamente).

Mercurio	1
Venus	2
Tierra	3
Marte	4
Júpiter	5
Saturno	6
Urano	7
Neptuno	8

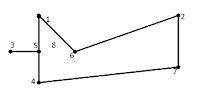
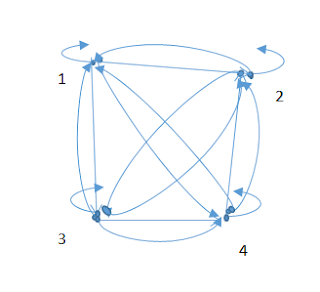
En los ejercicios 9 al 12 dibuje la digráfica de la relación.

9.-  La relación del ejercicio 4 en {a, b, c} 

10.-  La relación R = {(1, 2), (2, 1), (3, 3), (1, 1), (2, 2)} sobre  X ={1, 2, 3}

11.- La relación R = {(1, 2), (2, 3), (3, 4), (4, 1)} en {1, 2, 3, 4} 

12.- La relación del ejercicio 7

13.-

R= {(a, b), (a, c), (b, a), (b, d), (c, c), (c, d)}

14.-

R={(1,1),(2,2),(3,3)(3,5)(4,3),(4,4),(5,4),(5,5)}

15.-  R={ Ø}

16.-

R = {(b, c), (c, d), (d, d)}